Computational models used for flight simulation consist of a number of components. These typically include an aerodynamic model, a method to account for unsteady effects and a flight mechanics toolbox in order to model the aircraft response for given loads and moments. Often, the aerodynamic model is a tabular aerodynamic model. The tabular model contains the force and moment coefficients for a given parameter set covering the flight envelope, which are obtained by empirical or computational methods.

For commercial aircraft, the flight envelope can be quite large, with required data points of the order of millions. The aerodynamic tables must cover this in order to simulate manoeuvres. If CFD is used as the source of the aerodynamic data, it is clearly not feasible to have a solution for each parameter combination. A number of methods can be used to minimise the required number of calculations including: altering the resolution of the tables; decoupling certain parameters to reduce the number of dimensions; and using a mix of fidelities to calculate the loads and moments at points of high or low parametric sensitivity. It is necessary to understand the limitations these assumptions, among others, introduce to ensure adequacy for relevant manoeuvres.

For manoeuvres where the rates become significant, or where the aerodynamics begin to deviate from the linear regime, unsteady modelling is required. A number of approaches have been proposed for this including: the dynamic stability derivative model; Volterra theory; Indicial approaches; a State-space model; and the Surrogate-Based Recurrence Framework (SBRF). Although each of these have their own benefits, in practice the most widely used is that of the stability derivative model, originally proposed by Bryan. This model is based on the assumption that the load and moment coefficients can be broken down into a steady state component and an unsteady component (i.e. changes in the values are relative to the rate of the motion).

The dynamic stability derivatives relate the rates to the load and moments. The unsteady (rate) contribution can be found by multiplying the derivative with the corresponding motion rate. This contribution is then added to the static value, obtained from the tables. Dynamic derivatives can be calculated using forced periodic oscillations. The values of the derivatives are equal to the first Fourier coefficients of the Fourier series of the solution. Given this model consists of a steady and unsteady component due to instantaneous rates, it does not account for history effects which are also present for manoeuvres. As such, this approach can only be considered as quasi-steady.

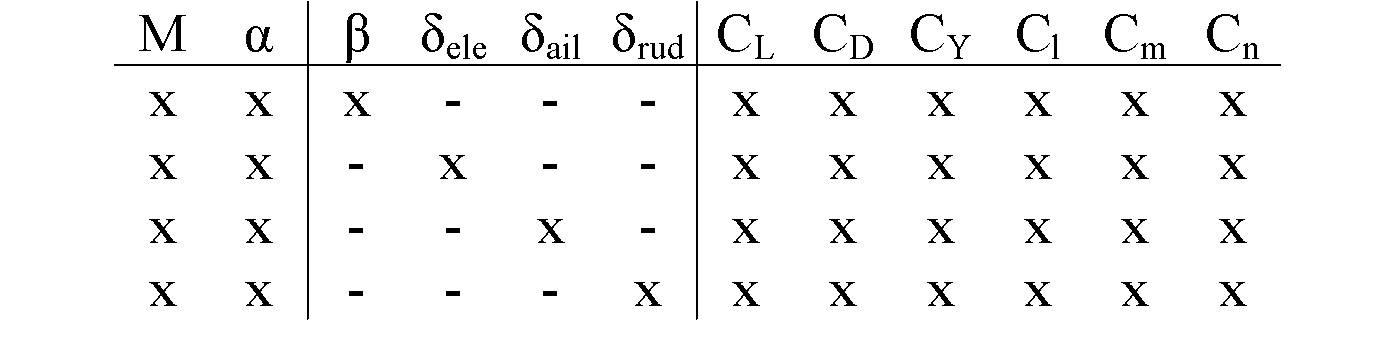
There are a number of examples where the tabular model is no longer adequate; but there has been little research to assess the fundamental assumptions in the formulation of this model, namely, resolution of tables, decoupling parameters, quasi-steady modelling and dynamics modelling. An assessment framework is used to understand the impact of each assumption. This framework consists of: defining a manoeuvre to be run; running the manoeuvre with a fully unsteady time-accurate CFD solver; running the same manoeuvre using the tabular model; and finally comparing the loads and moments from each, to determine any discrepancies and the reason for these.

Initial work has been carried out to assess the assumptions using a NACA 0012 aerofoil. The aerofoil on its own was used for a simple assessment, but has since been modified to include a 25% chord trailing edge flap. The addition of the flap introduces an extra dimension to the tables, and allows for free response calculations to be run for an assessment of applicability for control purposes. Four key regimes are of interest. These are shown for a two dimensional space in figure 1. A number of manoeuvres are defined to include all regimes, thus ensuring a comprehensive assessment of the assumptions through the flight envelope.

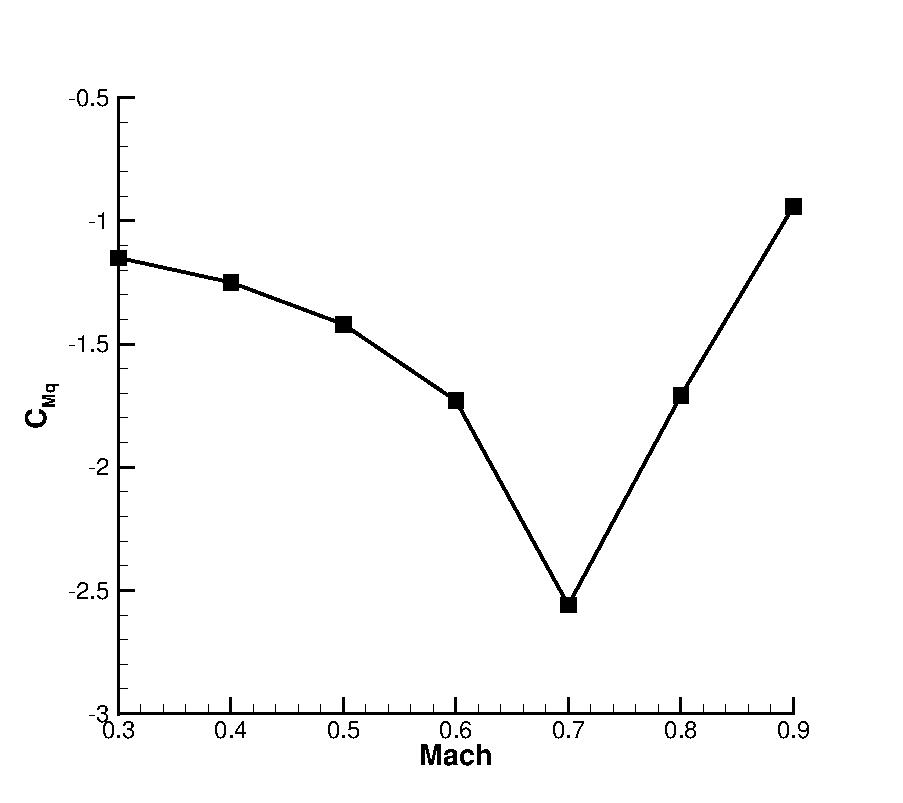
A final assessment is on the dynamic stability derivative model. When running a simulation, a single value of the derivative is used (i.e. assuming it does not change with the flight conditions). However, the value changes with Mach number, mean incidence, amplitude of oscillation and reduced frequency of the oscillation. This presents a problem for more extreme manoeuvres, where the unsteady component may be incorrectly predicted. It is therefore necessary to assess how this affects the predicted loads and moments for certain manoeuvres, and the uncertainty it introduces when using a single value.

Click on the following images to enlarge the view.

More details can be found in the following publications:

Refereed Journals

• McCracken, A., Da Ronch, A., Timme, S., and Badcock, K.J., "Solution of Linear Systems in Fourier-Based Methods for Aircraft Applications," International Journal of Computational Fluid Dynamics, Special issue Fourier Based Methods Development and Applications. 2012.
  link

Conference Papers

• McCracken, A., J., Kennett, D., Da Ronch, A., Badcock, K.J., "Assessment of Tabular Models Using CFD," AIAA Atmospheric Flight Mechanics Conference, Boston, Massachusetts, Aug. 2013.
  AIAA Paper 2013-4978

• McCracken, A., J., Akram, U., Da Ronch, A., and Badcock, K.J., "Requirements for Computer Generated Aerodynamic Models for Aircraft Stability and Control Analysis," 5th Symposium on Integrating CFD and Experiments in Aerodynamics (Integration 2012) , JAXA Chofu Aerospace Center, Tokyo, Japan, Oct. 2012.
  link

• McCracken, A., J., Timme, S., and Badcock, K.J., "Accelerating Convergence of the CFD Linear Frequency Domain Method by a Preconditioned Linear Solver," European Congress on Computational Methods in Applied Sciences and Engineering , Vienna, Austria, Sept. 2012.
  link

Presentations