Meshless Preprocessor and Solver
Title :
Investigators :
Partner :
Sponsor :
Development of a Meshless Preprocessor and Solver
Kennett, D.J., Angulo, J., Timme, S., and Badcock, K.J.
BAE Systems
UK Engineering and Physical Sciences Research Council (EPSRC)
Project Background
The project goal is to develop a meshless CFD method that solves the Navier-Stokes equations using only a distribution of points throughout the computational domain. The lack of the strict connectivity of cells that are associated with finite volume methods means that the meshless method is ideal for modelling flows with multiple bodies, which may move relative to one another, in a time accurate simulation. Point distributions can be generated around each body separately and then overlapped to form the domain; as a result, a preprocessor method is needed to select the stencils to be used by the solver. The solver/preprocessor methods form part of a combined code, used by the University of Liverpool, called Parallel MeshLess (PML).
Currently, the solver works for solving the Euler and RANS equations (with the 1 equation Spalart-Allmaras turbulence model) in two and three spatial dimensions. The equations are discretised in space using the meshless method, details of which can be found in the references, and the integration in time is performed implicitly, using analytical Jacobian matrices (with appropriate approximations) and a preconditioned Krylov subspace iterative method. Unsteady simulations are also possible in both the time domain and frequency domain using a linear frequency domain solver; Harmonic Balance functionality is implemented as well.
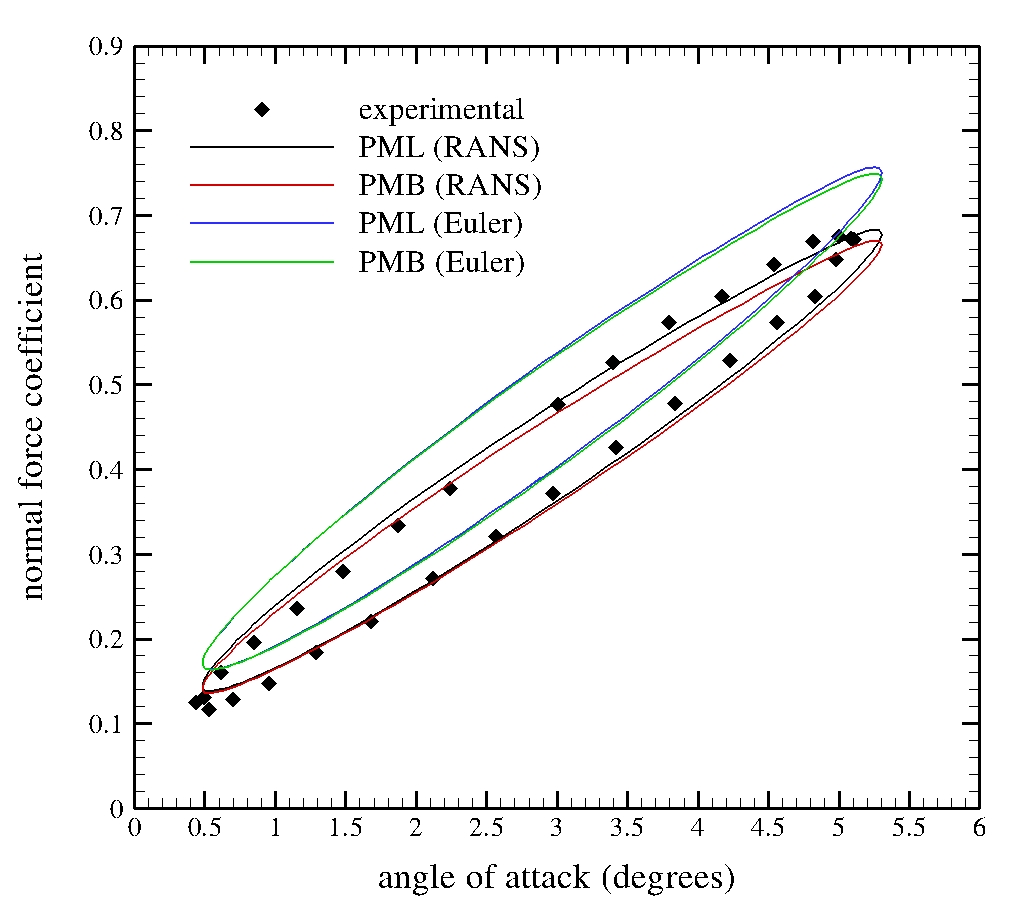
Flow solver results
Click on the following images to enlarge the view.
Meshless Preprocessor
A procedure is required to select the stencils from the points on which the solver can directly operate: this is one of the key challenges. This stage must be automatic, robust and efficient if the method is to be used in practical CFD calculations. The current code can be used on bodies that fully overlap in two and three dimensions; the stencils are selected using the concept of a resolving vector, which results in better quality stencils in high gradient regions of flow such as boundary layers.
One application is in control surface deflection. A simple unsteady example, in two-dimensions, is given in the animation below; this consists of a truncated NACA 0012 aerofoil (75% of the chord), which is one input domain, and a flap, which is another input domain, which overlaps the main body and can rotate around the centre of rotation at x=0.75c.
The simulation is inviscid, at Mach 0.3, and the control surface deflections are +/-5 degrees.
Another application is in store release; and a simple time-dependent, two-dimensional test case is given in the animations below; the case consists of a NACA 0012 aerofoil, with a smaller aerofoil (half the size) below, which acts as the store. The first animation shows the movement of the points during the simulation as the store slowly descends from the mains body; notice how the point distributions associated with each body slide over one another. The second animation shows the pressure contours for a laminar flow at Mach 0.5, with Reynolds number of 5000.
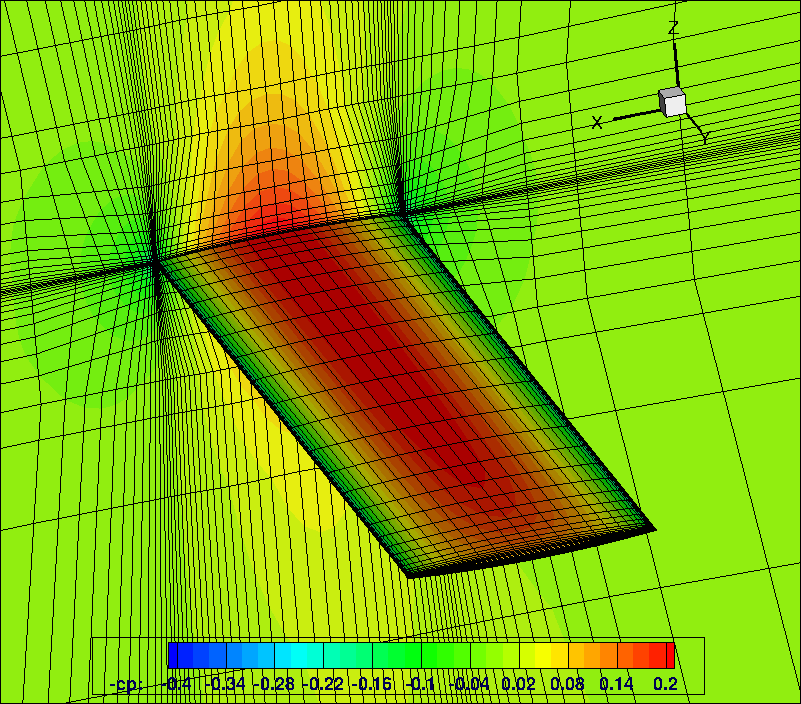
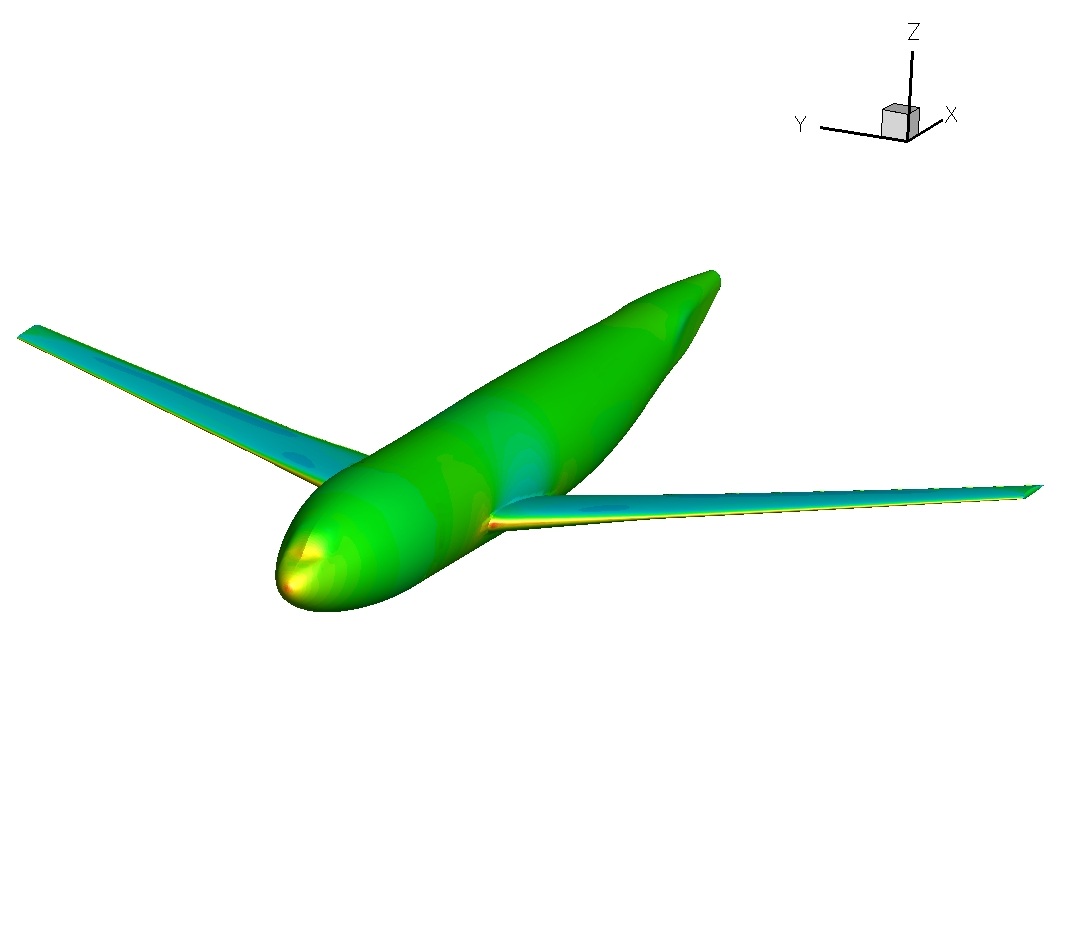
The ability of PML to produce a geometry from various component point distributions can be seen with the DLR-F6 case. This case has two input geometries: a fuselage and a wing; and the two are intersected to form the aircraft geometry. The intersection location is dealt with the automatic creation of triangles to rewrite the boundary; and the preprocessor
works on the resultant geometry and point locations.
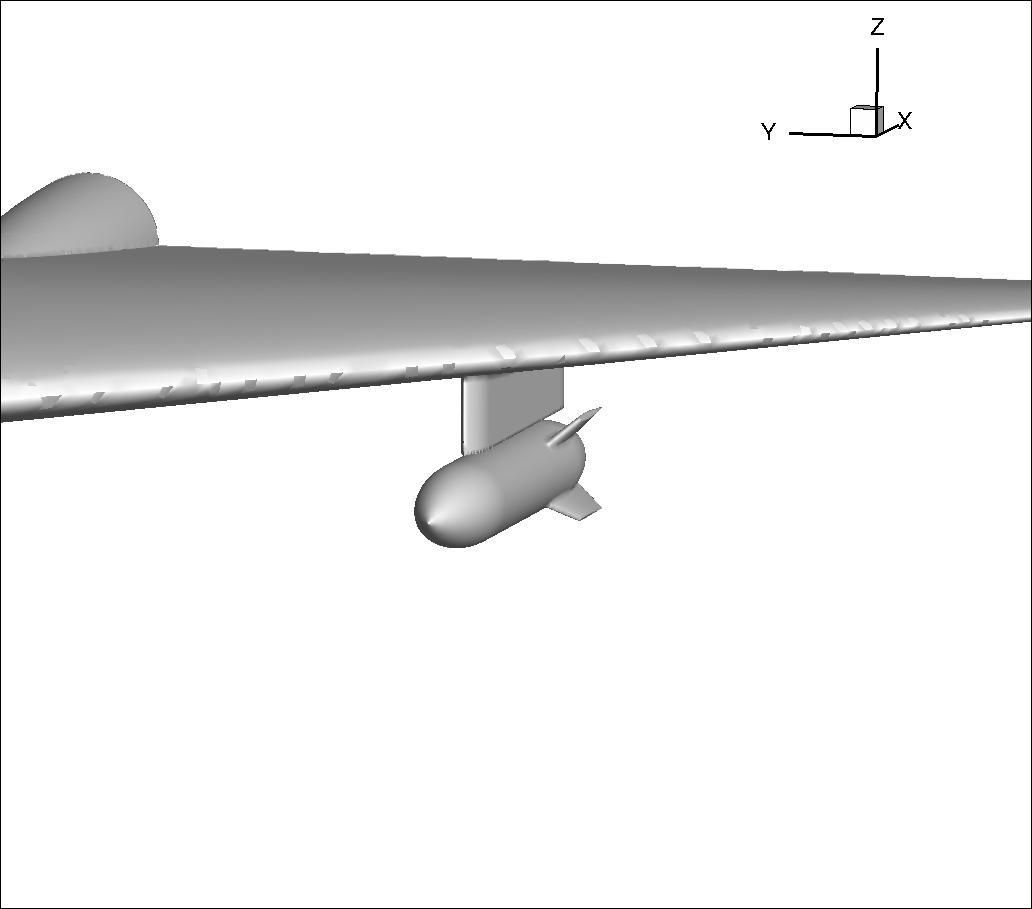
A three-dimensional store release from an aircraft can be seen in the Open Source Fighter test case below. This is a more complicated system, so the meshless method is utilised to create the geometry from individual components of the aircraft and store. To create the aircraft geometry, separate point distributions are generated around the fuselage, wing, tip store, horizontal and vertical stabilisers, and the pylon; the store geometry consists of the store body and four fins. Thus, a total of eleven input point distributions is used; and when the sub-domains are overlapped, the boundaries must be reallocated, the points internal to solid walls must be blanked, and then the stencils are selected that respect the boundary contours and can accurately capture the flow in question. For the first time step all of the bodies are touching; but for the subsequent steps the store geometry has separated, and the meshless method allows us to simulate this movement as the store descends.
The classic AGARD supersonic store release case is performed to test the meshless method in computing three-dimensional, moving body flows, which require a six-degree of freedom module to determine the location of the bodies at successive real-time steps. The computational domain consists of two input grids: a wing and the store, both in an unstructured grid format. The initial location of the bodies can be seen in the figures below, along with the store location after 0.1s and 0.2s. An animation of the store release can also be downloaded below.
Results using the preprocessor
Click on the following images to enlarge the view.
References
More details can be found in the following publications:
Refereed Journals
Kennett, D.J., Timme, S., Angulo, J., and Badcock, K.J., "Semi-Meshless Stencil Selection for Anisotropic Point Distributions," International Journal of Computational Fluid Dynamics, Vol. 26, Nos. 9-10, pag. 463-487, 2012.
doi: 10.1080/10618562.2012.744450Kennett, D.J., Timme, S., Angulo, J., and Badcock, K.J., "An Implicit Meshless Method for Application in Computational Fluid Dynamics," International Journal for Numerical Methods in Fluids, Vol. 71, No. 8, pag. 1007-1028, 2012.
doi: 10.1002/fld.3698
Conference Papers
Angulo, J., Kennett, D.J., Timme, S., and Badcock, K.J., "Parallel Semi-Meshless Stencil Selection for Moving Geometry Simulations," 21st AIAA Computational Fluid Dynamics Conference, San Diego, California, Jun. 2013.
AIAA Paper 2013-2854Kennett, D.J., Timme, S., Angulo, J., and Badcock, K.J., "Semi-Meshless Stencil Selection on Three-Dimensional Anisotropic Point Distributions with Parallel Implementation," 51st AIAA Aerospace Sciences Meeting, Grapevine, Texas, Jan. 2013.
AIAA Paper 2013-0867Kennett, D.J., Timme, S., Angulo, J., and Badcock, K.J., "An Implicit Semi-Meshless Scheme with Stencil Selection for Anisotropic Point Distributions," 20th AIAA Computational Fluid Dynamics Conference, Honolulu, Hawaii, 27-30 Jun. 2011.
AIAA Paper 2011-3234Timme, S., Badcock, K.J., Wu, M., and Spence, A., "Lyapunov Inverse Iteration for Stability Analysis using Computational Fluid Dynamics," 53rd AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference, Honolulu, Hawaii, 23-26 Apr. 2012.
AIAA Paper 2012-1563
Presentations
Kennett, D.J., "Development of a Meshless Method to Study Multibody Systems Using CFD," Advanced Technology Centre, BAE Systems, Bristol, U.K., March 2013.