Computational Aeroelasticity
Title :
Investigators :
Project Background
Transonic aeroelastic problems, including phenomena such as violent flutter and limit cycle oscillation, require computational fluid dynamics (CFD) methods for modelling the unsteady nonlinear aerodynamics, including shock waves, shock boundary layer interaction and separation.
CFD modelling has become feasible for the analysis of full aircraft configurations due to advances in algorithms and computing power over the last decades. However, in the aeroelastic context, reduced order modelling of the aerodynamics is an active area of investigation. This is due to the large number of analyses required for a single aircraft, covering all possible load conditions and aircraft/store configurations. Computational cost is the limiting factor. An alternative viewpoint to model reduction is the development of more efficient tools working with the full aerodynamic system instead.
Rather than solving the full unsteady nonlinear problem, the fluid dynamics equations are often linearised by introducing small perturbations leading to the frequency domain. Nonlinear transonic flow features are contained in the underlying steady flow solution, while dynamic perturbations about this nonlinear static equilibrium are linear. Linearising the aeroelastic problem gives an eigenvalue problem of the form A x = μ x.
To overcome several numerical challenges in solving the above eigenvalue problem for aeroelastic stability analysis encountered in early work using CFD aerodynamics, the so-called Schur complement rearrangement has been adapted. Specifically, the coefficient matrix A generally contains four matrix blocks with the two off-diagonal blocks describing the coupling between fluid and structure. The eigenvalues of interest for a flutter analysis emerge from the structural Jacobian matrix block. Block Gaussian elimination (with the fluid Jacobian matrix as pivot) gives the Schur complement of the coefficient matrix, and the large linear eigenvalue problem becomes a small nonlinear eigenvalue problem of the structural equations corrected for the aerodynamic influence. This rearrangement creates a problem very similar to the conventional, industry-standard, formulation. Applying interpolation techniques to the aerodynamic influence matrix provides an efficient method when solving the small aeroelastic eigenvalue problem.
Results
Click on the following images to enlarge the view.
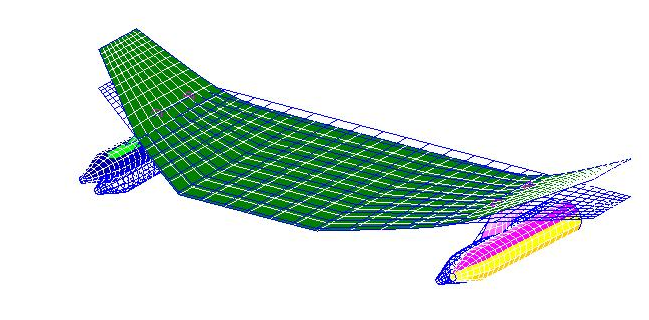
Goland wing/store configuration: representative element of aerodynamic influence matrix interpolated using Kriging.
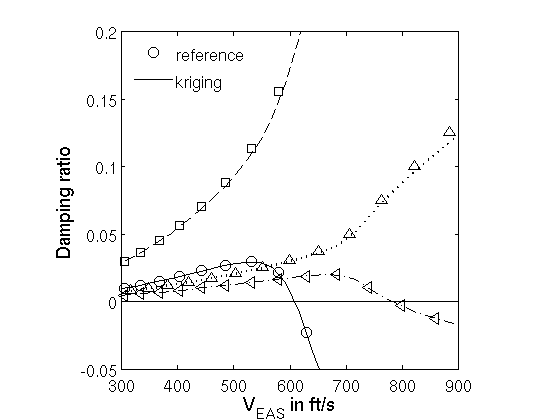
Open Source Fighter: matched point mode traces showing imaginary part of eigenvalue as function of altitude.
References
More details can be found in the following publications:
Refereed Journals
Badcock, K.J., Timme, S., Marques, S., Khodaparast, H.H., Prandina, M., Mottershead, J.E., Swift, A., Da Ronch, A., and Woodgate, M., "Transonic Aeroelastic Simulation for Envelope Searches and Uncertainty Analysis," Progress in Aerospace Sciences, Vol. 47, No. 5, pag. 392-423, 2011.
doi: 10.1016/j.paerosci.2011.05.002Timme, S., Marques, S., and Badcock, K.J., "Transonic Aeroelastic Stability Analysis Using a Kriging-Based Schur Complement Formulation," AIAA Journal, Vol. 49, No. 6, pag. 1202-1213, 2011.
doi: 10.2514/1.54550Timme, S., and Badcock, K.J., "Searching for Transonic Aeroelastic Instability Using an Aerodynamic Model Hierarchy," AIAA Journal, Vol. 49, No. 6, pag. 1191-1201, 2011.
doi: 10.2514/1.54596Timme, S. and Badcock, K.J., "Updating Computational Aeroelastic Models using Flight Flutter Test Data," International Journal of Aerospace and Lightweight Structures, Vol. 1, No. 2, pag. 157-178, 2011.
doi: 10.3850/S2010428611000183Marques, S., Badcock, K.J., Khodaparast, H.H., and Mottershead, J.E., "Transonic Aeroelastic Stability Predictions Under the Influence of Structural Variability," Journal of Aircraft, Vol. 47, No. 4, pag. 1229-1239, 2010.
doi: 10.2514/1.46971Badcock, K.J. and Woodgate, M.A., "Bifurcation Prediction of Large Order Aeroelastic Models," AIAA Journal, Vol. 48, No. 6, pag. 1037-1046, 2010.
doi: 10.2514/1.40961Woodgate, M. and Badcock, K.J., "On the fast prediction of Transonic Aeroelastic Stability and Limit Cycles," AIAA Journal, Vol. 45, No. 6, pag. 1370-1381, 2007.
doi: 10.2514/1.25604Badcock, K.J., Woodgate, M.A., and Richards, B.E., "Direct Aeroelastic Bifurcation Analysis of a Symmetric Wing Based on the Euler Equations," Journal of Aircraft, Vol. 42, No. 3, pag. 731-737, 2005.
doi: 10.2514/1.5323Badcock, K.J., Woodgate, M., and Richards, B.E., "Hopf Bifurcation Calculations for a Symmetric Airfoil in Transonic Flow," AIAA Journal, Vol. 42, No. 5, pag. 883-892, 2004.
doi: 10.2514/1.9584